

We can say that a rhombus is a kite but a kite may or may not be a rhombus. The main difference between a kite and a rhombus is that a rhombus has all equal sides whereas a kite has two pairs of adjacent equal sides. All sides of a rhombus are equal and opposite angles are equal. Is kite a rhombus?Ī kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other and only one pair of opposite angles are equal. If the base angles are equal, the trapezoid is a special type called an isosceles trapezoid. Trapezoids are quadrilaterals that have one pair of parallel sides. Similarly, every kite is not a parallelogram, because the opposite sides of a kite are not necessarily parallel.

This definition is equivalent to the following one: A kite is quadrilateral that has two pairs of equal adjacent sides. The most general definition that is typically used: A kite is a quadrilateral in which one of its diagonals is its axis of symmetry. Most kites have three main components: the kite body (which comes in many different shapes and sizes), the bridle (or harness), and the control line (or tether). What are the 3 main components of a kite?Ī kite is a heavier-than-air object that flies… just like an airplane. The longer diagonal of a kite bisects the shorter one. The intersection of the diagonals of a kite form 90 degree (right) angles. So it has all the properties of a kite and a parallelogram.
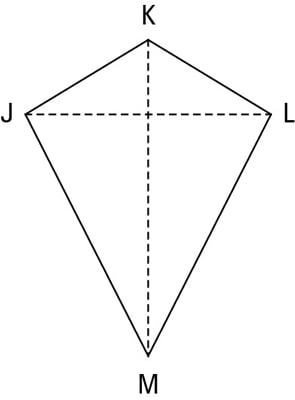
Which one has all the properties of a kite and a parallelogram?Īnswer : In a rhombus the opposite sides are parallel, diagonals bisect at right angles and all the sides are equal. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite to each other instead of being adjacent. In Euclidean geometry, a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other. What is the properties of kite in geometry? Other important polygon properties to be familiar with include trapezoid properties, parallelogram properties, rhombus properties, and rectangle and square properties. Kite properties include (1) two pairs of consecutive, congruent sides, (2) congruent non-vertex angles and (3) perpendicular diagonals. The area of the kite is 1/2 * d 1 * d 2.The kite can be viewed as a pair of congruent triangles with a common base.Angles opposite to the main diagonal are equal.Kite has 2 diagonals that intersect each other at right angles.A kite is symmetrical about its main diagonal.The longer or main diagonal bisects the other diagonal.It has 2 diagonals that intersect each other at right angles.It can be viewed as a pair of congruent triangles with a common base.The two angles are equal where the unequal sides meet.The longer diagonal of the kite bisects the shorter diagonal.The diagonals of a kite are perpendicular to each other.

The important properties of the kite are as follows. In two dimensions it refers to the angle formed by two intersecting lines, such as at a “corner” (vertex) of a polygon.Īnd (3) perpendicular diagonals. In geometry, a vertex is an angle (shape) associated with a vertex of an n-dimensional polytope.


 0 kommentar(er)
0 kommentar(er)
